

License: CC BY-SA: Attribution-ShareAlike t graph.ĬC licensed content, Specific attribution The velocity of an object at any given moment is the slope of the tangent line through the relevant point on its x vs.
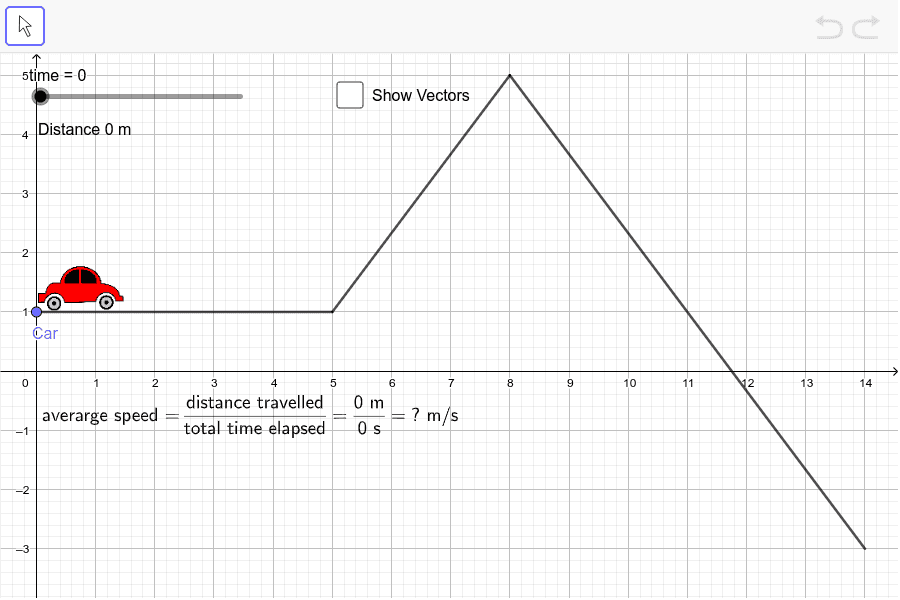
If we extend this line, we can easily calculate the displacement of distance over time and determine our velocity at that given point. That line would be the line tangent to the curve at that point. To do this, we find a line that represents our velocity in that moment, shown graphically in. In order to determine our velocity at any given moment, we must determine the slope at that point. One way is to look at our instantaneous velocity, represented by one point on our curvy line of motion graphed with distance vs. Since our velocity is constantly changing, we can estimate velocity in different ways. However, changing velocity it is not as straightforward. To calculate the speed of an object from a graph representing constant velocity, all that is needed is to find the slope of the line this would indicate the change in distance over the change in time. This would result in a curvy line when graphed with distance over time. Motion with Changing Velocity: Motion is often observed with changing velocity. Therefore, your average velocity, or displacement over time, would be 0 m/s.
#Gta 5 the game free full
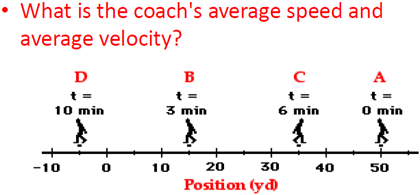
Because you walked in a full rectangle and ended up exactly where you started, your displacement is 0 meters. When calculating average velocity, however, you are looking at the displacement over time. From this, you would get an average speed of 14/30 = 0.47 m/s. If you are calculating average speed, you would calculate the entire distance (3 + 4 + 3 + 4 = 14 meters) over the total time, 30 seconds. You walk three meters north, four meters east, three meters south, and another four meters west. Imagine you are walking in a small rectangle. To illustrate the difference between average speed and average velocity, consider the following additional example. To get more details, we must consider smaller segments of the trip over smaller time intervals. For example, we cannot tell from average velocity whether the airplane passenger stops momentarily or backs up before he gets to the back of the plane. The average velocity of an object does not tell us anything about what happens to it between the starting point and ending point, however. The minus sign indicates that the average velocity is also toward the rear of the plane. Suppose, for example, an airplane passenger took five seconds to move -4 m (the negative sign indicates that displacement is toward the back of the plane ). The SI unit for velocity is meters per second, or m/s, but many other units (such as km/h, mph, and cm/s) are commonly used.
In contrast, average velocity is defined as the change in position (or displacement) over the total time of travel.Īverage Velocity: The kinematic formula for calculating average velocity is the change in position over the time of travel. This distinction becomes more apparent when we calculate average speed and velocity.Īverage speed is calculated as the distance traveled over the total time of travel. Velocity, on the other hand, is a vector quantity and so has both magnitude and direction. Speed is a scalar quantity and has only magnitude. In physics, however, they are distinct quantities. In everyday usage, the terms “speed” and “velocity” are used interchangeably. velocity: A vector quantity that denotes the rate of change of position with respect to time, or a speed with a directional component.Average velocity is different from average speed in that it considers the direction of travel and the overall change in position.The average velocity of an object does not tell us anything about what happens to it between the starting point and ending point.Average velocity can be calculated by determining the total displacement divided by the total time of travel.Next time you are out walking, imagine you are still and it is the world that moves under your feet. Think about this: are you really standing still? You are on planet Earth which is spinning at 40,075 km per day (about 1675 km/h or 465 m/s), and moving around the Sun at about 100,000 km/h, which is itself moving through the Galaxy. When we say something is "at rest" or "moving at 4 m/s" we forget to say "in relation to me" or "in relation to the ground", etc. Yes, the velocity is zero as you ended up where you started. Velocity = 130 m 100 s East = 1.3 m/s East You forgot your money so you turn around and go back home in 120 more seconds: what is your round-trip speed and velocity? Example: You walk from home to the shop in 100 seconds, what is your speed and what is your velocity?


 0 kommentar(er)
0 kommentar(er)
